前回の記事で予告した記事が遅くなってしまった。申し訳ない。
ここでは、Pythonの疎行列ライブラリscipy.sparseについて、データの内部構造を説明する。内部構造を知らずにブラックボックスとして使いたい場合は前回の記事を参照のこと。
はじめに(あるいは前回記事のまとめのまとめ)
scipy.sparseで疎行列を表すクラスは主に以下のものがある(他にもあるが、ここではとりあげない。これだけ知ってれば大体のことはできる。)
- lil_matrix
- csr_matrix
- csc_matrix
通常は、lil_matrixを用意してそこに値を詰めてから、csr_matrixまたはcsc_matrixに変換してから計算を行う。csr_matrixとcsc_matrixのどちらを使うかは以下のことから判断する。
- 演算はcsr同士またはcsc同士が高速
- csrは行を取り出すのが高速
- cscは列を取り出すのが高速
- csrは転置をとるとcscになり、cscは転置をとるとcsrになる
内部構造
以下csr_matrixとcsc_matrixのデータ内部構造について説明する。このCSRとCSCという形式は、Pythonに限定された話ではなく、数値計算で疎行列を扱うときに一般的に使われるものである。
用語
以下、行と列の名前は、行0, 行1, 行2, …, 列0, 列1, 列2, …という風に0からナンバリングして呼ぶことにする。「i行目」「j列目」というときも、0を起点として考える。
csr_matrix
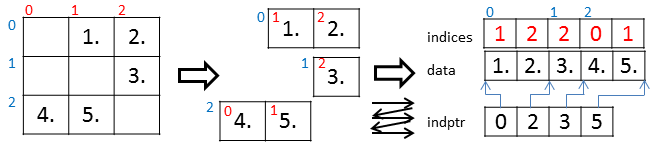
内部データは、3つのメンバ変数data, indices, indptrで構成される。
- dataには行方向に非ゼロ要素の値が格納される。(dataのサイズは非ゼロ要素の数)
- indices[j]はdata[j]が何列目の要素かを示す。(indicesのサイズはdataのサイズに等しい)
- jがindptr[i]以上indptr[i+1]未満の範囲にあるときに、data[j]およびindices[j]はi行目の要素である。つまりindptrはdataおよびindicesにおいて、どこからどこまでが同じ行かを示す。(indptrのサイズは行列の行数+1)
上図の行列で、行0、行1、行2にはそれぞれ、2個、1個、2個の非ゼロ要素がある。したがって、dataおよびindicesは両方とも2,1,2のサイズに区切り、それぞれの行の情報を格納する。行0の非ゼロ要素の値は1., 2.だからdata[0], data[1]には1., 2.が格納され、行0の非ゼロ要素の列インデックスは1,2だから、indices[0], indices[1]には1,2が格納される。行0の情報はdata[0]とindices[0]から始まるので、indptr[0]には0が入り、行1の情報はdata[2]とindices[2]から始まるので、indptr[1]には2が入る。以下同様に格納される。
実際の実行セッションは以下のようになる。
>>> from scipy.sparse import lil_matrix, csr_matrix
>>> a=lil_matrix((3,3))
>>> a[0,1]=1.; a[0,2]=2.; a[1,2]=3.; a[2,0]=4.; a[2,1]=5.
>>> b=a.tocsr()
>>> b.todense()
matrix([[ 0., 1., 2.],
[ 0., 0., 3.],
[ 4., 5., 0.]])
>>> b.indices
array([1, 2, 2, 0, 1], dtype=int32)
>>> b.data
array([ 1., 2., 3., 4., 5.])
>>> b.indptr
array([0, 2, 3, 5], dtype=int32)
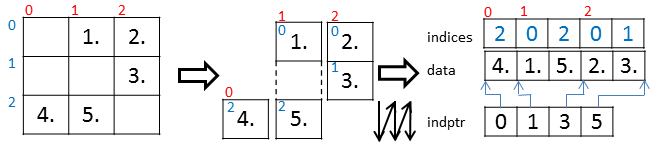
csc_matrix
csr_matrix同様に内部データは、3つのメンバ変数data, indices, indptrで構成される。csrの説明で、「行」と「列」を入れ替えるとcsc_matrixの内部構造の説明になる。つまり以下のようなことになる。
- dataには列方向に非ゼロ要素の値が格納される。(dataのサイズは非ゼロ要素の数)
- indices[j]はdata[j]が何行目の要素かを示す。(indicesのサイズはdataのサイズに等しい)
- jがindptr[i]以上indptr[i+1]未満の範囲にあるときに、data[j]およびindices[j]は列iの要素である。つまりindptrはdataおよびindicesにおいて、どこからどこまでが同じ列かを示す。(indptrのサイズは行列の列数+1)
内部構造を知っていると何がうれしいか
内部構造を理解することで、高速な操作ができるケースがある。非ゼロ要素に同一関数を作用させるケースについては以前のブログで書いたが、ここではコンストラクタの高速化の話をする。
例えば新しく、行列をつくるとき、(公式ドキュメントのユースケースにかかれているように)lil_matrixに詰めてからcsr_matrix(またはcsc_matrix)に変換するよりも、csr_matrix(またはcsc_matrix)の内部構造を直接用意してコンストラクトしたほうが処理速度が速い。
実際に、次のような行列について、初期化にどのくらいかかるかのベンチマークを取ってみる。
\[
\begin{pmatrix}
2&1& & &\cr
&2&1& &\cr
& &\ddots&\ddots&\cr
& & &\ddots&1 \cr
& & & &2
\end{pmatrix}
\]
ベンチマークに使ったコードは以下の通り。ここではサイズ10000×10000の行列で実験している。
from scipy.sparse import lil_matrix, csr_matrix
import numpy as np
from timeit import timeit
def set_lil(n):
a=lil_matrix((n,n))
for i in xrange(n):
a[i,i]=2.
if i+1<n:
a[i,i+1]=1.
return a
def set_csr(n):
data=np.empty(2*n-1)
indices=np.empty(2*n-1,dtype=np.int32)
indptr=np.empty(n+1,dtype=np.int32)
# to be fair, for-sentence is intentionally used
# (using indexing technique is faster)
for i in xrange(n):
indices[2*i]=i
data[2*i]=2.
if i<n-1:
indices[2*i+1]=i+1
data[2*i+1]=1.
indptr[i]=2*i
indptr[n]=2*n-1
a=csr_matrix((data,indices,indptr),shape=(n,n))
return a
print "lil:",timeit("set_lil(10000)",
number=10,setup="from __main__ import set_lil")
print "csr:",timeit("set_csr(10000)",
number=10,setup="from __main__ import set_csr")
そして、ある環境における実行結果が以下の通り。
lil: 11.6730761528 csr: 0.0562081336975
csr_matrixに直接詰めたほうが圧倒的に速い。とはいえ、csr_matrixに直接詰めるコードの方が複雑になるので、開発効率の面からlil_matrixを利用する選択肢も捨てがたいかと思う。csr_matrix(またはcsc_matrix)に直接詰めるのが有効なのは以下のような場合かと考えられる。
- 疎行列を何度も用意しなければいけない場合(一度用意するだけならあまりパフォーマンスの違いは気にならないかもしれない)
- データがあらかじめある程度ソートされた形で用意されている場合(オンラインアルゴリズムのような、次にどの非ゼロ要素がくるかわからないような状況だと、lil_matrixを使ったほうが手っ取り早いし、そこでわざわざソートするのならパフォーマンスの優位性は薄れる)
まとめ
- scipy.sparseを使うとき、通常はlil_matrixを用意して値を入れて、csr_matrixかcsc_matrixに変換してから計算する。そのように使っている限りは内部構造を知る必要はなく、ブラックボックスとして使える。
- しかし場合によっては、csr_matrixやcsc_matrixに直接値を詰めたり、中身をいじったりするほうが、計算速度が速くなる。そのためには内部データ構造を理解する必要がある。
追記:
2015/4/1 csc_matrixの図が間違っていたので修正しました。指摘していただいた@KeWata09さんに感謝します。